01

大家好，我是吴玲利，来自武汉经济技术开发区新城小学。是朱乐平名师工作站“一课研究”团队第5组的成员，很高兴和您在此相遇。

02

1.听一听:让学生做儿童数学家

2.读一读:触及数学的本质 激发学习的潜能

3.开心一笑

03

04

一、教学内容

人教版六年级上册第42页例7及相应的“做一做”和练习

二、教学目标

1.会把一个整体看作”1”,根据分率解决有关工程问题的应用题。

2.通过借助线段图培养学生分析问题、解决问题的能力和认真审题的习惯。

重点:利用假设法掌握工程问题的解题思路和方法。

难点:理解假设不同的数据得出相同结果的道理

三、教学过程

(一)复习旧知

(1)修一条360米的公路，甲队修12天完成，平均每天修多少米? (数量关系式是什么)

工作总量÷工作时间=工作效率

(2)修一条360米的公路，甲队每天修18米，多少天能完成?

工作总量÷工作效率=工作时间

(3)加工一批零件，计划8小时完成，平均每小时加工这批零件的几分之几?

(这里的1指什么)把工作总量看作单位“1”

(4)打印一份稿件，小明每天完成 ，几天可以完成?

(5)修一段36千米的路，甲队单独修需要12天完成，乙队单独修需要18天完成,甲、乙合修几天可以完成?

工作总量÷工作效率和=合作时间

师:像上面的修路、加工零件、打印稿件等工作，这些统称为工程，今天我们就一起来研究“工程问题”。

(二)研究新知

1.阅读与理解。

(1))出示例7主题图:

这条道路，如果我们一队单独修，12天能修完。如果我们二队单独修，18天能修完。如果两队合修，多少天可以修完?

(2)师:这里要解决多少天可以修完?解决问题的三大步骤你还记得吗?

生:阅读与理解、分析与解答、回顾与反思 (师:你记得真牢固)

(3)谁能大声地把题目读一读。

师:通过读题，你知道了哪些信息?

师:这两队之间有什么关系?(同修一条路)

师:这里要求的是什么?(合作的时间)你认为合作时间怎样求?

2、分析与解答。

(1)你会解答吗?不会解答的同学你觉得有什么困难?

师:要解决“两队合修，多少天修完?”需要知道哪些信息?

工作总量(这条路的总长度)和工作效率和

预设:要求天数还需要一些条件，但题目中没有。

这条路的总长度不知道。一队和二队每天修多少米不知道。

两队合修每天修多少米不知道。

(2)我们需要的这两个信息题目中都没有给，怎么办?

小组内先讨论2分钟。

(3)有讨论结果了吗?

方法一:假设这条路的长度。

师:假设总长是多少呢，是随便取一个数吗?我们取的数最好计算比较简单，仔细读题中的已知条件，假设多少比较合适呢?(最好是12和18的最小公倍数)为什么?除36外，你还能找到其他计算比较简单的数据吗?(72、180、……)板书:

假设这条路有36米，假设这条路有72米，假设这条路有180米。算出一队和二队每天修的米数。

方法二:把这条路的全长看作“1”。

(4)师:每个小组先组内讨论一下，你们准备用哪种方法解决这道题。每个小组先组内讨论，你们准备用哪种方法解决这道题。请同学们以小组为单位，分工合作，完成下面的表格。

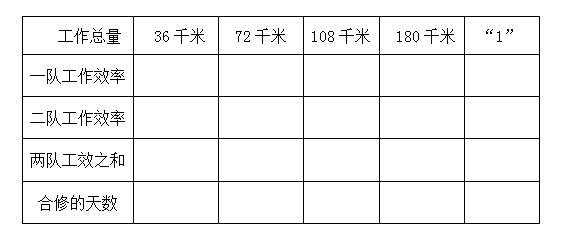
(教师利用现代化手段--教学助手拍下学生较典型的做法)

学生完成后，各小组上台交流汇报。

(5)师:我拍下了不同的解题方法。你能对照上面的表格说一说你的思路吗?

师:还有不同的方法。

(老师在黑板上一一填表格完成)

(6)通过上面的计算，你发现了什么?(不同的假设，计算结果都一样吗?这是为什么呢?)

生:假设这条路的长度。假设这条路有36米，假设这条路有72米，假设这条路有180米，算出天数是一样的。如果把这条路看作“1”算出的天数也是一样的。(不管假设这条道路有多长，答案都是相同的)

师:工程问题，如果总量没有告诉我们一个具体的数，我们可以假设一个总数。还可以把总量用“1”表示。为了计算简便，一般我们都把总量看作“1”进行计算。

无论假设公路全长是多少，他们每天修了这条路的几分之几没有变化。

(三)回顾反思

我们来检验一下答案的合理性。

上一篇：高中化学新课程改革对传统教学思想的挑战及教
下一篇：没有了